3.4. Цикли з лічильником
3.42. Задані натуральне число n,
дійсні числа ![]() . Скласти алгоритм для знаходження:
. Скласти алгоритм для знаходження:
а) max(![]() ); б) min(
); б) min(![]() );
);
в) max(![]() ); г) min(
); г) min(![]() );
);
д) min(![]() )+max(
)+max(![]() );
);
е) max( ![]() ); ж) max(
); ж) max(![]() ;
;
з) ![]() .
.
Розв`язок а)
Позначивши через А чергове число, яке ми вводимо, а через Min - min(![]() ), складемо слідуючий алгоритм:
), складемо слідуючий алгоритм:
Алг
Мінімум це
змін i,N:нат;
A,Min:дійсн;
поч
взяти(N);
взяти(A); Min¬A;
для
i¬1 до N повт
взяти(A);
якщо
A<Min то Min¬A кр
кц;
показати(Min)
ка.
3.43. Дано натуральне число n, цілі числа ![]() . Скласти алгоритм знаходження
. Скласти алгоритм знаходження
а) min(![]() );
);
б) min(![]() );
);
в) max(![]() );
);
г) кількості парних серед ![]() ;
;
д) кількості повних квадратів серед ![]() ;
;
е) кількості квадратів непарних чисел серед ![]() .
.
Розв`язок. в).
Позначимо через А - чергове число, що вводиться, Р - добуток
введених чисел ![]() , що передують А, включаючи саме це число, Max -
шуканий максимум. Складемо алгоритм у вигляді:
, що передують А, включаючи саме це число, Max -
шуканий максимум. Складемо алгоритм у вигляді:
Алг
Max_P це
змін N,i :нат;
А,Р,Мах
:ціл;
поч
взяти(N);
взяти(А);
Р¬А; Мах¬А;
для
і¬2 до N повт
взяти(А);
Р¬Р*A;
якщо
Р>Max то Мах¬Р кр
кц;
показати(Мах)
ка.
3.44. Дано натуральне число n. Скласти
алгоритм обчислення факторіала y=n!, використовуючи
а) суцільний зростаючий; б)
суцільний спадний цикли з лічильником.
3.45. Скласти алгоритм обчислення подвійного
факторіала натурального числа n y=n!!.
Розв`язок. За означенням
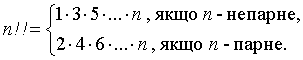
В обох випадках ми маємо як
співмножники всі члени спадної арифметичної прогресії з різницею -2, які містяться між n та 1. Звідси
Алг
Факт2 це
змін
k,n :нат;
y:дійсн;
поч
взяти(n);
y¬1;
для
k¬n до 1 через -2 повт
y¬y*k
кц;
показати(y)
ка.
розв`язує дану задачу. Зауважимо, що при непарному n останнім
значенням k буде 1, а при парному - 2. Приклад виконання алгоритму
наведений в табл. 3.2
Таблиця
3.2. Трасувальна таблиця до завдання 3.45.
|
|
n |
y |
k |
|
взяти(n) |
5 |
|
|
|
y¬1 |
|
1 |
|
|
для k¬5 до 1 через -2 повт |
|
|
|
|
k=5 |
|
|
5 |
|
y¬y |
|
5 |
|
|
k=3 |
|
|
3 |
|
y¬y |
|
15 |
|
|
k=1 |
|
|
1 |
|
y¬y |
|
15 |
|
|
кц |
|
|
|
|
показати(y) |
|
15 |
|
3.46.
Скласти алгоритми обчислення факторіалів:
а) y=(2n)!!; б) y=(2n+1)!!; в) y=n!n!!(n+1)!!
3.47. Задане натуральне
число n. Скласти алгоритми обчислення добутків
а) P=![]() ; б)P=
; б)P=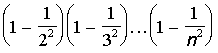 , n>2
, n>2
3.48. Скласти алгоритм друку таблиці значень функції y=sin(x)
на відрізку [0,1] з кроком h=0.1.
3.49. Скласти алгоритм визначення кількості тризначних натуральних
чисел, сума цифр яких дорівнює n (n>=1). Операцію ділення не
використовувати.
3.50. Дано n цілих чисел. Скласти
алгоритм, що визначає, скільки з них більші за своїх "сусідів", тобто
попереднього та наступного чисел.
3.51. Задані натуральне число n,
дійсні числа ![]() . Скласти алгоритм визначення
. Скласти алгоритм визначення
а) max(![]() ), де
), де 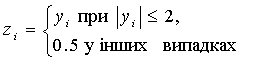 ;
;
б) min(![]() ), де
), де 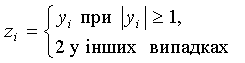 ;
;
в) ![]() , де
, де  .
.
Розв`язок в).
Позначивши через S шукану суму, а через y значення чергового введеного числа, подамо алгоритм
розв`язку задачи в наступному вигляді:
Алг Сума_Z це
змін i,n
:нат;
y,z,S
:дійсн;
поч
взяти(n); S¬0;
для i¬1 до n повт
взяти(y);
якщо
(y<10) & (y>0) то z¬y
інакше z¬1
кр;
S¬S+z
кц;
показати(S)
ка.