3.3. Цикли за умовою
3.21.
Для довільного цілого числа m>1 знайти найбільше ціле k, при
якому 4k<m.
3.22. Для заданого натурального числа n одержати найменше
число вигляду 2r, яке перевищує n.
3.23. Визначити із скількох
від`ємних чисел починається задана послідовність чисел.
3.24. Задана непорожня послідовність ненульових цілих чисел, за
якою йде 0. Визначити кількість змін знаку в цій послідовності. Наприклад, у послідовності 1, -34, 8, 14, -5, 0 знак змінююється три
рази.
Розв`язок .
алг Зміна_Знаку_2 це
змін k:нат ;
a,x:ціл;
поч
взяти(x,a); k¬0;
{цикл за умовою повторення}
поки a<>0
повт
якщо a*x<0
то k¬k+1
кр ;
x¬а;
взяти (а)
кц;
показати(k)
ка.
Замінимо цикл з умовою повторення
відповідно на цикл з умовою закінчення та цикл з виходом. Модифіковані
алгоритми приймуть вигляд
алгоритм Зміна _Знаку_2 це
змін k:нат;
a,x:ціл;
поч
взяти(x,a); k¬0;
{цикл з умовою закінчення}
якщо a<>0 то
повт
якщо
a*x<0
то k¬k+1
кр;
x¬a;
взяти(a)
до a=0
кц
кр;
показати(k)
ка.
алгоритм Зміна_Знаку_3 це
змін k:нат;
a,x:ціл;
поч
взяти(x,a);k¬0;
{цикл з виходом}
цикл
якщо a=0
то вихід ;
якщо a*x<0 то
k¬k+1
кр;
x¬a;
взяти(a)
кц;
показати(k)
ка.
3.25. Дана непорожня послідовність різних натуральних чисел, за
якою слідує 0. Визначити порядковий номер найменшого з них.
3.26. Дана непорожня послідовність різних дійсних чисел, серед яких є хоча б одне від`ємне
число, за якою йде 0. Визначити величину найбільшого серед від`ємних членів
цієї послідовності.
3.27.
Маємо дійсне число a. Скласти алгоритми обчислення:
а) серед чисел ![]() першого, більшого за a;
першого, більшого за a;
б) такого найменшого n,
що ![]()
3.28.
Скласти алгоритми обчислення:
а) номера
найбільшого числа Фібоначчі, яке не перевищує задане число a;
б) номера найменшого числа
Фібоначчі, яке більше заданого числа a;
в) суми всіх чисел Фібоначчі, які не перевищують 1000.
3.29. Дана непорожня послідовність з натуральних чисел, за якою йде
0. Обчислити суму тих з них, порядкові номери яких - числа Фібоначчі.
3.30. Скласти алгоритми для обчислення найменшого додатнього члена
числових послідовностей, які
задаються рекурентними співвідношеннями, та його номера
а) xn=xn-1+xn-2+100,
x1=x2=-99, n=3,4,...;
б) xn=xn-1+xn-2+xn-3+200, x1=x2=x3=-99, n=4,5,...;
в) xn=xn-1+xn-3+100, x1=x2=x3=-99, n=4,5,...
Розв`язок а) Оскільки послідовність xn задана рекурентним співвідношенням другого порядку, то для
обчислення довільного елементу послідовності потрібні три змінні.
Нехай змінна u пробігає послідовність xk, k=1,2,....Тоді,
в якості умови завершення циклу будемо розглядати умову u>0.
Її заперечення - це умова u<=0
яка і розглядається як умова повторення циклу. Одержуємо алгоритм
алгоритм Мінім_елемент це
змін u,v,w:ціл;
поч
u¬-99,v¬-99; {u=x1,
v=x2}
поки u<=0 повт
w¬u+v+100;u¬v;v¬w
кц;
показати(u)
ка.
3.31. Скласти алгоритм, який з`ясовує, чи входить задана цифра до запису заданого
натурального числа.
3.32. Скласти алгоритм "обернення" (запису в оберненому
порядку цифр) заданого натурального числа.
Вказівка. Для
побудови числа використати рекурентне співвідношення y0=0, yi=yi-1*10+ai, де ai
- наступна цифра
числа n при розгляді цифр справа наліво.
3.33. Скласти алгоритм, який визначає потрібний спосіб розміну
будь-якої суми грошей до 99 коп. за допомогою монет вартістю 1, 2, 3, 5,
10, 15, 20, 50 коп.
3.34. Скласти алгоритми наближеного обчислення суми всіх доданків, абсолютна
величина яких не менше e>0
:
а) 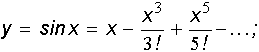
б) 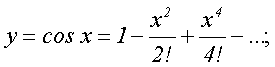
в) 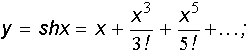
г) 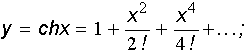
д) 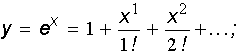
е) 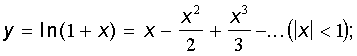
ж)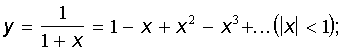
з) 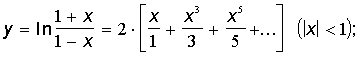
і) ![]()
к) ![]()
л) ![]()
м) ![]()
н) ![]()
о) 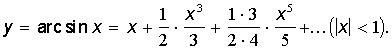
Вказівка. Суму y обчислювати за
допомогою рекурентного співвідношення S0=0,
Sk=Sk-1 + ak,
k=1,2,... , де ak - k-тий
доданок, для обчислення якого також складається рекурентне співвідношення. В
якості умови повторення циклу розглядається умова ![]() e.
e.
Розв`язок в)
Рекурентне співвідношення для знаходження ak має вигляд a1=x, ak+1=ak*x2/(2*k*(2*k+1)), k=1,2,...
Передбачивши захищене введення для завдання e,
одержимо наступний алгоритм
алгоритм Сінус_гіпербол це
змін k:ціл;
x,y,z,a,eps:дійсн;
поч
повт
взяти(x,eps)
до eps>0
кц;
k¬0;a¬x;z¬x*x;y¬0;
поки abs(a)>=eps повт
k¬k+1;y¬y+a;a¬a*z/(2*k*(2*k+1))
кц;
показати(y)
ка.
3.35. Маємо дійсні числа x,e
(x¹0 ,e>0). Обчислити з точністю e нескінченну суму і вказати кількість
врахованих доданків.
а) 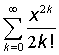 ; б)
; б) 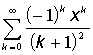 ;
;
в) 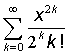 ; г)
; г) 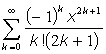 .
.
3.36. Маємо ціле n>2. Скласти алгоритм для обчислення всіх
простих чисел з діапазону [2,n].
Розв`язок.
Нехай змінна m приймає послідовно значення цілих чисел з діапазону
[2,n]. Тоді m буде простим числом , якщо воно не має дільників в діапазоні [2,![]() ].
Враховуючи цю обставину, складаємо алгоритм
].
Враховуючи цю обставину, складаємо алгоритм
алгоритм Прості_числа це
змін k,n,m:нат;
p:бул;
поч
повт
взяти(n);
до n>2
кц;
m¬2;
поки m<=n повт
p¬n;k¬2;
поки
p&(k*k<=n) повт
p¬n
mod k<>0;
якщо p то k¬k+1
кр
кц;
якщо p то показати(m,' просте') кр;
m¬m+1
кц
ка.
3.37. Скласти алгоритм друку всіх простих дільників заданого
натурального числа.
3.38. Скласти алгоритм, який визначає чи є задане натуральне число n досконалим, тобто рівним сумі всіх своїх
(додатніх) дільників, крім самого цього числа (наприклад, число 6 - досконале: 6=1+2+3 ).
Вказівка. Шукаємо
суму S всіх дільників заданого числа n. Якщо S=n, то
число, яке перевіряємо, є досконалим. Перша ідея полягає в знаходженні дільників числа n в діапазоні [1, n div 2]. У
відповідності з другою ідеєю пошук ведеться тільки між 1 та ![]() і якщо дільник
знайдений, то до суми S додаються як дільник, так і частка.
і якщо дільник
знайдений, то до суми S додаються як дільник, так і частка.
3.39. Дано натуральне число k . Скласти алгоритм одержання к-тої
цифри послідовності
а) 110100100010000 ... , в якій
виписані підряд степені 10;
б) 123456789101112 ... , в якій
виписані підряд всі натуральні числа;
в) 149162536 ... , в якій
виписані підряд квадрати всіх натуральних чисел;
г) 01123581321 ... , в
якій виписані підряд всі числа Фібоначчі.
3.40. Скласти алгоритм знаходження кореня рівняння tg x=x на
відрізку [0,001;1,5] із заданою точністю e, використовуючи метод ділення відрізку
навпіл.
Розв`язок.
алг корінь це
змін x,l,r,eps:дійсн;
поч
повт
взяти (eps)
до eps>0;
l ¬0.001; r ¬1.5;
{лівий та правий кінці відрізка з
коренем: tg(l)<l,tg(r)>r}
повт
x ¬(l+r)/2; {середина
відрізка [l,r]}
якщо
sin(x)/cos(x)<x то
l ¬x {[l,r]¬[x,r]}
інакше
r ¬x {[l,r]¬[l,x]}
кр
до l-r<eps
кц;
x ¬ (l+r)/2;
{корінь - середина останнього відрізка [l,r]}
показати (х)
ка.
3.41. Знайти корінь рівняння ![]() = 0, який
міститься на відрізку [0,2], з заданою точністю e.
= 0, який
міститься на відрізку [0,2], з заданою точністю e.
Вказівка.
Одним з методів розв`язування рівняння є метод хорд, який полягає в обчисленні
елементів послідовності
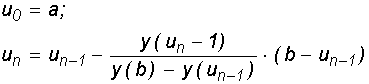
до виконання умови ![]() . В умовах нашої задачі а=0, b=2,
. В умовах нашої задачі а=0, b=2, ![]() .
.