3.2. Програмування рекурентних
співвідношень
3.9. Скласти алгоритми для обчислення елементів послідовностей
а) ![]() ; д)
; д)
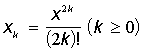 ;
;
б) 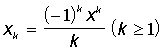 ; е)
; е)  ;
;
в)  ; ж)
; ж)
![]() ;
;
г) ![]() ; з)
; з) 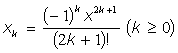 .
.
Розв`язок г) Складемо
рекурентне співвідношення для обчислення xk
x0=x,
xk=![]() , k=1,2...
, k=1,2...
Передбачивши введення і
виведення, отримаємо
алг
Рекур це
змін
х,у:дійсн;
і,п:нат;
поч
взяти
(х,п);
у¬1;і¬0;
повт
п раз
і¬і+1;
у¬у*х/і
кц;
показати (у)
ка.
3.10. Числами Фібоначчі називається числова послідовність {Fn},
задана рекурентним співвідношенням другого порядку
F0=0;
F1=1; Fk=Fk-1+Fk,
k=2,3,...
Скласти алгоритм для
обчислення Fn
Розв`язок.Якщо
змінна f буде пробігати послідовність Фібоначчі, то двох додаткових змінних sf і t буде достатньо для позначення
наступних двох чисел
Алг
Фібоначчі це
змін
n,f,sf,t:нат;
поч
взяти (п);
f¬0;sf¬1;
{f =F0, sf =F1}
повт
п раз
t¬f+sf;
f¬sf;sf¬t
кц;
{f =Fn,
sf=Fn+1}
показати
(f)
ка.
3.11. Скласти алгоритм обчислення
довільного члена послідовностей, які задані рекурентними співвідношеннями:
а) xn=xn-1+xn-3, x0=x1=1,
x2=2, n=3,4,...;
б) xn=2xn-1+3xn-2, x0=0,
x1=9, n=2,3,...;
в) xn=xn-1+xn-2+xn-3, x0=x1=1,
x2=6, n=3,4,...;
г) xn=xn-1+4xn-3, x0=x1=x2=2, n=3,4,...;
д) xn=xn-1*(xn-2+1), x0=1,
x1=1, n=2,3,...;
е) xn=![]() , x0=0,
x1=
, x0=0,
x1=![]() , n=2,3,...;
, n=2,3,...;
3.12. Скласти алгоритми для обчислення сум:
а) Sn=![]() ;
;
б) Sn =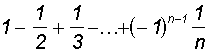 ;
;
в) Sn =![]() ;
;
г) Sn =![]() ;
;
д) Sn =1-2-3+4-5-6+...+(3n-2)-(3n-1)-3n;
е) Sn =1+2+3+...+n; ж) Sn
=a+2a2+3a3+...+nan;
з) Sn = ; і) Sn
=
; і) Sn
=![]() ; к) Sn
=
; к) Sn
=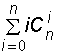 ;
;
л) Sn = ; м) Sn =
; м) Sn =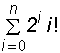 ; н) Sn
=
; н) Sn
=![]() ;
;
о) Sn =![]() ; п) Sn =
; п) Sn =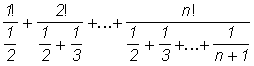 .
.
Вказівки. Суму Sn обчислити за допомогою рекурентного співвідношення
S0=0, Sk=Sk-1+ak,
k=1,2,...n, де ak - k-тий доданок.
з) Si=2Si-1+i2; і) Sn =2n; л) Sn =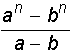 ;
м) ak =2kak-1.
;
м) ak =2kak-1.
3.13. Скласти алгоритми для обчислення добутків:
а) 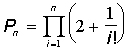 ; б)
; б)  ;
;![]()
в)  ; г)
; г) 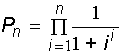 .
.
Вказівка.
Добуток Pn обчислити за допомогою рекурентного
співвідношення P0=1; Pk=Pk-1*ak, k=1,2,...,n, де ak - k- тий множник.
3.14. Скласти алгоритми для обчислення ланцюгових дробів
а)  ;
;

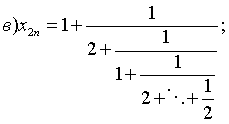
Вказівка.
Використати рекурентні
співвідношення
а) b0=b, bk=b+![]() , k=1,2,...n;
, k=1,2,...n;
в) b0=4n+2, bk=4(n-k)+2+![]() , k=1,2,...n.
, k=1,2,...n.
3.15. Скласти алгоритми для обчислення
а) многочлена
Чебишова
T0(x)=1, T1(x)=x,
Tn(x)=2xTn-1(x) - Tn-2(x), n=2,3,...;
б) многочлена
Ерміта
H0(x)=1, H1(x)=2x,
Hn(x)=2xHn-1(x) - 2(n-1)Hn-2(x), n=2,3,...
заданого степеню n в точці х.
3.16. Скласти алгоритм обчислення
довільного елемента послідовностей, заданих рекурентними співвідношеннями
а) v0=1,v1=0.3, vi=(i+2)vi-2 , i=2,3,...
б) v0=v1=v2=1, vi=(i+4)(vi-1 - 1)+(i+5)vi-3 , i=3,4,...
в) v0=v1=0,v2=![]() , vi=
, vi= , i=3,4,...
, i=3,4,...
3.17. Скласти алгоритм обчислення
довільного елемента послідовності vn,
визначеної системою співвідношеннь
v0=v1=1, vi = 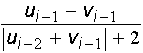 , i=2,3,..;
, i=2,3,..;
де u0=u1=0 , ui =  , i=2,3,... .
, i=2,3,... .
3.18. Скласти алгоритм для обчислення сум
а) Sn = , де a1=0, a2=1, ak=ak-1+k*ak-2, k=3,4,...;
, де a1=0, a2=1, ak=ak-1+k*ak-2, k=3,4,...;
б) Sn =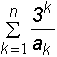 , де a1=1, a2=1, ak=
, де a1=1, a2=1, ak= ![]() , k=3,4,...;
, k=3,4,...;
в) Sn = , де a1=1, a2=1, ak=
, де a1=1, a2=1, ak=![]() , k=3,4,...;
, k=3,4,...;
г) Sn =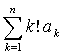 , де a1=0, a2=1, ak=ak-1+
, де a1=0, a2=1, ak=ak-1+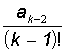 , k=3,4,...;
, k=3,4,...;
д) Sn = , де a1=a2=a3=1, ak=ak-1+ak-3, k=4,5,...;
, де a1=a2=a3=1, ak=ak-1+ak-3, k=4,5,...;
е) Sn =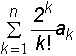 , де a0=1, ak=kak-1+
, де a0=1, ak=kak-1+![]() , k=1,2,...
, k=1,2,...
Вказівка.
Позначимо загальний член ряду через bk.
Послідовність аk задається залежностями вигляду (R1) для е), (R2) для а)--г) та (R3) для д); Sk=g(Sk-1, bk).
Значення аk будуть обчислюватись за
теоремами 1-2. Для обчислення послідовновності Sk цикли доповнюються однією змінною.
Розв`язок
д). Вводячи допоміжну змінну для обчислення
2k і використовуючи рекурентні співвідношення t0=1, tk=2tk-1, k=2,3,.. для знаходження цієї системи отримаємо алгоритм
алг Сума це
змін
u , v, w, t, r, s: дійс;
n:
нат;
поч
взяти
(n);
u¬1; v¬1; w¬1; t¬1;
s¬0;
{
u=a1,
v=a2,
w=a3 }
повт n раз
t¬t*2;
s¬s+u/t;
r¬u+w; u¬v;
v¬w;
w¬r
кц;
показати
(s)
ка.
3.19. Скласти алгоритми для обчислення сум
а) Sn = ,
,
де 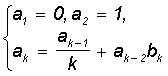 ,
, 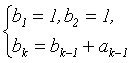 ; k=3,4,...;
; k=3,4,...;
б) Sn =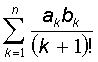 ,
,
де 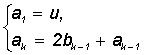 ;
; 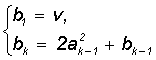 ; k=2,3,...;
; k=2,3,...;
u,v - задані дійсні числа;
в) Sn =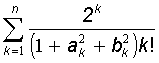 ,
,
де 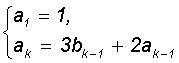 ;
; 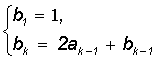 ; k=2,3,...;
; k=2,3,...;
г) Sn =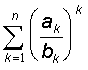 ,
,
де 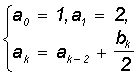 ;
; 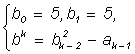 ; k=2,3,...;
; k=2,3,...;
д) Sn =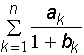 ,
,
де 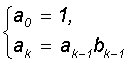 ;
;  ; k=1,2,... .
; k=1,2,... .
Розв`язок
д). Послідовності {an} і {bn}
задані рекурентним співвідношеннями першого порядку, проте залежність перехресна.
Використовуємо по одній допоміжній змінній для кожної з послідовностей.
Отримаємо алгоритм
алг Сума
це
змін
a, b, aa, bb, s:дійс;
n:нат;
поч
взяти
(n);
a¬1;
b¬1; s¬0,5;
повт
n раз
aa¬a*b;
bb¬a+b;
a
¬aa; b¬bb; s¬s+a/(1+b)
кц;
показати
(s)
ка.
Неважко побачити, що змінну
bb легко виключити.
3.20. Скласти алгоритми для обчислення добутків
а) 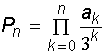 , де
, де 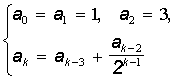 , k=3,4,...;
, k=3,4,...;
б)  ,
,
де 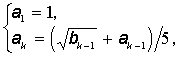
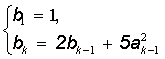 , k=2,3,... .
, k=2,3,... .
Розв`язок
а) Послідовність {an} задана рекурентним співвідношенням
третього порядку. Для обчислення її довільного елемента ak використаємо теорему 2. Тоді добуток Pn обчислюється за допомогою рекурентного співвідношення P0=1,
Pk=Pk-1*![]() , де zk -- к-тий степінь числа 3,
визначений із співвідношень z0=1, zk=zk-1*3.
Передбачивши також
змінну t для обчислення степеня 2к-1, отримаємо алгоритм
, де zk -- к-тий степінь числа 3,
визначений із співвідношень z0=1, zk=zk-1*3.
Передбачивши також
змінну t для обчислення степеня 2к-1, отримаємо алгоритм
алг Добуток
це
змін
a0, a1, a2, w, p, z, t:дійсн;
n:нат;
поч
взяти (n);
a0¬1; a1¬1;
a2¬3;
z¬1;
p¬1;
t¬2;
повт n раз
z¬z*3; p¬p*a1/z;
t¬t*2;
w¬a0+a1/t;
a0¬a1; a1¬a2;
a2¬w
кц;
показати
(p)
ка.