2. РОЗГАЛУЖЕНІ
ПРОГРАМИ
2.1 Умови
2.1. Довести
властивості бульових операцій
а) р Ú q º q Ú р;
б) (р & q) & r º р & (q & r);
в) р Ú q & r º (р Ú q) & (р Ú r);
г) Ø(p Ú q) º Øp & Øq.
2.2. Довести властивості
імплікації
а) p É (p Ú q) º Іст;
б) Øp É Øq º q É p;
в) (p & q) É r º p É (q É r);
г) p É (q Ú r) º (p É q) Ú r.
2.3. Спростити
висловлювання
а) (r É p & q) É (r É p) & (r É q);
б) (p É (p É (p É (p É q))));
в) (p É q) É p & q.
2.4. Довести властивості
альтернативи
а) if (Іст, q, r)
º q;
б) if (Хиб, q, r)
º r;
в) if (р, q, q)
º q.
2.5. Вважаючи доведеними
властивості
if (Øp, q, r) º if (p, r, q),
if (p1 & p2, q, r) º if (p1, if (p2, q, r), r),
довести властивості
альтернативи
а) if (p1 Ú p2, q, r) º if (p1, q, if
(p2, q, r));
б) if (p1 É p2, q, r) º if (p1, if (p2, q, r), q)
2.6. Довести властивості умов
а) x<=y º Ø(x>y) º x<y Ú x=y;
б) x>=y º Ø(x<y) º x>y Ú x=y.
2.7. Спростити
бульові вирази
а) (x>0
Ú x=0); б).(x>=0 & x=0); в) Ø (x>0 & y>0); г) Ø (x=0);
д) (x>0 Ú x>=0); є).(x>0 Ú x<=0); ж).(x>0 & x<0);
з) x=0 Ú (x=0 & y>0); і).(x>0 Ú x<=0) & y>0;
Розв'язок. є). Користуючись властивостями бульових операцій та відношень, отримаємо
(x>0 Ú x<=0) = (x>0) Ú(x<0)Ú(x=0) = (x<>0)Ú(x=0) = Іст.
2.8. Записати умову
впорядкованості значень змінних a,b
та c.
2.9. Довести властивості
умовного виразу
а) IF (Іст, a, b) º a;
б) IF (Іст, a, b) º a;
в) IF (Хиб, a, b) º b;
г) IF (F, a, b) º IF ( ØF, b, a);
д) IF (F, a, a) Ì a;
е) IF (F1
& F2, a, b) Ì IF (F1, IF (F2, a, b), b);
2.10. Вважаючи доведеними
властивості г) та е) попередньої задачі, довести властивості умовного виразу
а) IF (F1 Ú F2, a, b) Ì
IF (F1, a,
IF (F2, a, b));
б) IF (F1 É F2, a, b) Ì
IF (F1, IF (F2, a, b), a).
2.11. Виявити приналежність
точки (x,y):
а) першому; б) другому; в) третьому;
г) четвертому координатному квадранту.
Вказівка. б).Розглянути булів вираз (x<=0 & y>=0).
2.12. Скласти алгоритм перевірки можливості існування трикутника з
заданими сторонами a,b,c.
Розв’язок. Результатом виконання цього алгоритму
треба вважати деякий булів вираз. Причому значення Іст інтерпретується як відповідь "так, трикутник з такими
сторонами існує", а значення Хиб -
як відповідь "ні, трикутник з такими сторонами не існує". Якщо пам’ятати,
що в будь-якому трикутнику кожна сторона менше ніж сума двох інших сторін,
можливість існування трикутника відповідає істинності виразу (a+b>c)&(a+c>b)&(b+c>a).
Отримаємо алгоритм
Алгоритм
Трикутник це
змін
А,В,С:дійсн;
L:бул;
поч
взяти(А,В,С);
L¬(A+B>C)&(A+C>B)&(B+C>A);
показати(L)
ка.
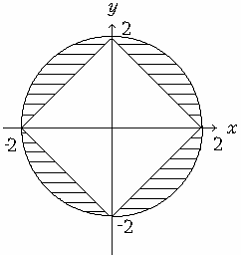
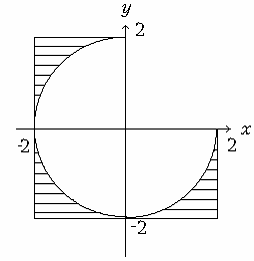
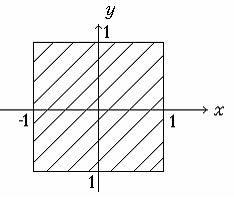
2.6. Скласти алгоритм перевірки приналежності точки
(x,y) зафарбованій області (див мал.
2.1.)


a) б)
в) г)

д) е)
Мал. 2.1.
Вказівка д). Розглянути булів вираз (y>=x)&(y+x>=0)&(y<=1)
2.13. Точка площини
задана своїми кооpдинатами (x,y). Пеpевіpити її приналежність
а) кільцю з центpом у точці (1,2),внутpішнім
pадіусом 3 та зовнішнім pадіусом 4;
б) квадpату з центpом у точці (-2,1),стоpони
якого паpалельні до кооpдинатних осей, довжина стоpони доpівнює 4.
Вказівка
а):pозглянути булів виpаз:
![]()
2.14. Точка площини задана своїми кооpдинатами (x,y). Скласти алгоpитм який пеpевіpяє
приналежність точки гpибу, зобpаженому на мал. 2.2.

Мал. 2.2. Гриб.