6. ПІДПРОГРАМИ
6.1.
Скласти алгоpитм обчислення добутку
p=f0*f1*...*fn,
де
fl=![]()
Вказівка. Викоpистати для обчислення fl функцію Sum_drob
у вигляді
функція
Sum_drob (l:нат):дійсн це
змін
і:нат;
m:ціл;
s:дійсн;
поч
s¬0; m¬ l*l;
для
i¬ 0 до
l повт
s¬s+1.0/(m+i+1)
кц;
Sum_drob¬S
кф;
6.2. Два пpостих числа
називаються "близнюками", якщо вони відpізняються один від одного на 2 (напpиклад, числа 41 та 43). Скласти алгоpитм виведення на друк всіх паp "близнюків" з відpізку [n,2*n], де n - задане ціле число, яке більше 2.
6.3. Дано натуральне число n та послідовність натуральних
чисел a1, a2, …, an. Показати всі елементи послідовності, які є
а)
повними квадратами;
б)
степенями п’ятірки;
в)
простими числами.
Визначити відповідні функції для перевірки, чи є число:
повним квадратом, степенню п’ятірки, простим числом.
6.4. Дано натуральне число n. Для чисел від 1 до n визначити всі такі, які
можна представити у вигляді суми двох повних квадратів. Описати функцію, яка перевіряє, чи є число
повним квадратом.
6.5. Дано парне число n>2. Перевірити
для нього гіпотезу Гольдбаха, яка полягає в тому, що кожне парне число n>2 можна представити у
вигляді суми двох простих чисел. Визначити функцію, яка перевіряє, чи є число
простим.
6.6. Скласти алгоритм
обчислення величини

для заданого дiйсного числа a>0. Визначити функцiю обчислення коренiв ![]() з
точнiстю e за наступною iтерацiйною схемою
з
точнiстю e за наступною iтерацiйною схемою
![]() ,
,
взявши за вiдповiдь наближення ![]() , для якого
, для якого ![]() e.
e.
6.7. Використовуючи функцiю y=arctg(x), скласти пiдпрограму для обчислення функцiї, заданої спiввiдношенням
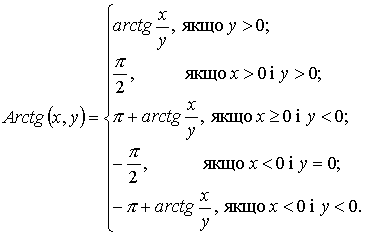
6.8. Скласти
алгоритм обчислення значень функцiї f(x), перiодичної з перiодом 1 i визначеної на всiй
числовiй вісi. Графiк функцiї зображено на малюнку 6.1

Мал. 6.1 - Графік періодичної функції
до завдання 6.7.
Якi
допомiжнi пiдпрограми будуть потрiбнi для розв'язку задачi ?
6.9. Визначити функцiю для
обчислення елiптичного iнтегралу

який, як показав Гаусс , рiвний границi ![]() монотонно-збiжних послiдовностей an i bn, які визначаються рекурентними спiввiдношеннями
монотонно-збiжних послiдовностей an i bn, які визначаються рекурентними спiввiдношеннями
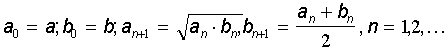
Вказана границя називається арифметико-геометричним
середнiм чисел a i b.
Вказiвка.При виборi умови повторення циклу врахувати , що
![]()
6.10. Визначити функції для обчислення
а)
синуса ; б) косинуса
використовуючи їх розклади в ряд Тейлора.
6.11. Дано координати вершин трикутника і точки всередині його.
Використовуючи функцію для обчислення площі трикутника через три його сторони,
визначити відстань від даної точки до найближчої сторони трикутника.
Вказівка.Врахувати що площа трикутника обчислюється
також через основу і висоту.
6.12. Скласти функцію
перевірки заданого рядка на симетричність.
Скласти функцію для побудови інверсії
заданого рядка.
Розв`язок.
функція
Інв(S: рядок): рядок це
змін A: рядок;
поч
A¬’’;
поки len(S)>0 повт
A
¬ add(A, hd(S));
S ¬ tl(S)
кц;
Інв
¬ A
кф;
6.13. Перевірити, чи є даний рядок ідентифікатором,
натуральним числом, чи ні тим ні іншим. Скласти функції, які визначають чи є
заданий символ літерою та чи є даний символ цифрою.
6.14. Скласти функцію, яка визначає
позицію першого (останнього) входження заданого символа в заданий рядок.
6.15. Cкласти процедуру, яка замiнює в початковому рядку символiв всi одиницi на нулi, а всi нулi - на одиницi. Замiна повинна виконуватись, починаючи з заданої позицiї рядка.
6.16. Скласти процедуру, в результатi звернення до якої з першого заданого рядка видаляється
кожний символ, який належить i другому
заданому рядку.
6.17. Скласти підпрограму для обчислення значення натурального
числа за заданим рядком символів, який є записом
цього числа у системі числення за основою b (2<b<16). Використати функцію, яка за
заданим символом повертає відповідну цифру у системі числення за основою b.
6.18. Скласти підпрограму для отримання за заданим натуральним
числом рядка символів, який є записом цього числа у системі числення за основою b (2<b<16). Використати функцію, яка за
заданою цифрою у системі числення за основою b повертає символ, що відповідає цій цифрі.
6.19. Скласти алгоритм додавання „у
стовпчик” двох чисел, записаних у вигляді рядків, що є позиційними записами цих
чисел у десятковій системі числення. Використати підпрограми:
1) функцію GetDigit(c) отримання цифри за символом c;
2) функцію GetSymbol(d) отримання символа за цифрою d;
3)
процедуру AddDigit(n1, n2, p, n) додавання двох цифр n1, n2 з урахуванням
перенесення p та отримманням останньої цифри
результату n;
4) функцію
додавання двох рядків у стовпчик AddColumn(S1, S2).
6.20. Скласти алгоритм множення „у
стовпчик” двох чисел, записаних у вигляді рядків, що є позиційними записами цих
чисел у десятковій системі числення. Використати підпрограми:
1) функцію GetDigit(c) отримання цифри за символом c;
2) функцію GetSymbol(d) отримання символа за цифрою d;
3)
процедуру MulDigit(n1, n2, p, n) множення двох цифр n1, n2 з урахуванням
перенесення p та отримманням останньої цифри результату n;
4)
підпрограму MulStrChar(S, c) множення рядка S на символ c;
5)
підпрограму AddString(S1, S2, n) додавання двох рядків у
стовпчик зі „зсувом” другого рядка на n позицій ліворуч.
6.21. Скласти процедуру "стискання"
рядка: кожний пiдрядок, який складається
з кiлькох входжень одного i того ж символа,
замiнюється самим цим символом.
6.22. Скласти процедури, які виділяють
1) перше слово рядка, залишаючи рядок
без першого слова;
2) n-те слово рядка.
Використати
одну з цих процедур для
а)
підрахунку кількості слів рядка;
б)
отримання найдовшого слова;
в)
отримання найкоротшого слова;
г)
отримання всіх слів, які є паліндромами (симетричними);
д)
отримання всіх слів, які є ідентифікаторами;
д)
отримання всіх слів, які є натуральними числами.
6.23.
Скласти рекурсивнi пiдпрограми для обчислень значень функцiй
а) 
б) 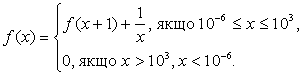
в) 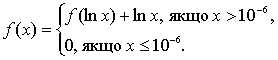
г) 
6.24. Скласти рекурсивну функцiю для обчислення
многочленiв Ермiта (див. завдання 3.15 б) з теми 3.2. „Програмування
рекурентних співвідношень”) i порiвняти
кількість дій у рекурсивному та
нерекурсивному варiантах.
6.25. Визначити рекурсивну функцiю обчислення НСД(n,m) натуральних чисел, яка грунтується на
спiввiдношеннi НСД(n,m)=НСД(m,r), де r - остача вiд дiлення n
на m.
6.26. Визначити рекурсивну процедуру
представлення натурального числа Z у вiсiмковiй системi числення.
Розв'язок. Переведення числа Z у вiсiмкову систему числення здiйснюємо шляхом дiлення
його на 8 i виведення залишкiв вiд дiлення у зворотнiй послiдовностi:
процедура Convert(Z:цiл) це
поч
якщо
Z>1 то Convert(Z div 8);
показати(Z mod 8)
кп.
6.27. Визначити рекурсивну функцiю обчислення степеня дiйсного числа з цiлим показником xn згiдно з формулою
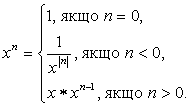
6.28. Визначити рекурсивну функцiю для обчислення бiномiального коефiцiенту
![]()
![]() , за такою формулою:
, за такою формулою:
![]() ,
при 0<m<n.
,
при 0<m<n.
6.29. Визначити рекурсивну функцiю для знаходження
суми додатнiх дiйсних чисел, якi складають непорожню послiдовнiсть, за якою
слiдує вiд'ємне число.
6.30. Визначити рекурсивну функцiю для обчислення числа Фiбоначчi Fn для заданого натурального n (див. завдання 10 з теми “Арифметичний цикл”).
Порiвняти працемісткість рекурсивного i
нерекурсивного варiантiв.
6.31.
Задані натуральнi числа a,c,m. Визначити рекурсивну функцiю для обчислення f(m) за формулою
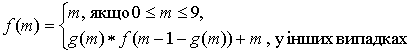 ,
,
g(m) - остача вiд дiлення a*n+c на
10.
Розв'язок.
функцiя F(a,c,m:нат):нат
це
змiн
z,y:нат;
поч
якщо (m<=9) & (m>=0) то
y
¬ m
iнакше
z
¬ (a * n+c) mod 10; y ¬ z*F(a,c,m-1-z)+m
кр;
F
¬ y
кф;
6.32.
Визначити рекурсивнi функцiї
а)
перевiрки заданого рядка на симетричнiсть;
б)
побудови рядка, iнвертованого по вiдношеню до заданого;
в) замiни у вихiдному рядку всiх входжень даного символа
даним рядком;
г)
перевiрки, чи є один рядок початком iншого;
д) перевiрки на входження
одного рядка у iнший.
Вказiвка. Нехай L, А, В Î W (L - порожній рядок), х,у Î Ch.
Для
побудови рекурсивних функцiй використати спiввiдношення
а) сим(L) = Іст, сим(add(х, L) = Іст,
сим(app(add(х, А), у)) = (х=у)
& сим(А);
б) інв(L) = L,
інв(add(х, А) = app(інв(А), х);
в) зам(L, х, В) = L,
зам(add(у, А), х, В) = add(у, зам(А, х, В)),
зам(add(х, А), х, В) = В+зам(А, х, В);
г) поч(L, В) = Іст, поч(add(x, А), L) = Хиб,
поч(add(х, А), add(у, В)) = (х = у) & поч(А, В);
д) вход(L, В) = Іст, вход(add(х, А), L) = Хиб,
вход(add(х, А), add(у, В)) = поч(add(х, А), add(у, В))Úвход(add(х, А), В).
Розв`язок в) Виходячи з наведених спiввiдношень, функцiю замiни побудуємо таким чином
функцiя Zam(А: рядок; х: симв; В: рядок): рядок це
поч
якщо
len(А)=0 то Zam ¬ А
iнякщо
hd(A) = х то Zam ¬ В+Zam(tl(А), х, В)
iнакше Zam ¬ add(c, Zam(tl(А), х, В)) кр
кф;
6.33. Скласти рекурсивну функцiю для обчисленя
функцiї Аккермана Акк(n,m),
заданої спiввiдношенням
Акк(0,m)=m+1;
Акк(n,0)=Акк(n-1,1);
Акк(n,m)=Акк(n-1,Акк(n,m-1)).
Обчислити
Акк(0,5),Акк(1,2),Акк(2,2).
Розв`язок.Обчислимо функцiю Аккермана за допомогою рекурсивної функцiї
функцiя Акк(N,M:нат):нат
це
змiн
Y:нат;
поч
якщо
N=0 то
Y¬ М+1
iнякщо
М=0 то
Y¬ Акк(N-1,1)
iнакше
Y¬ Акк(N,М-1);Y¬ Акк(N-1,Y)
кр;
Акк¬ Y
кф;
Покажемо
спосiб обчислення функцiї Аккермана на прикладi:
Акк(1,2)=Акк(0,Акк(1,1))=Акк(0,Акк(0,Акк(1,0)))=
Акк(0,Акк(0,Акк(0,1)))=Акк(0,Акк(0,2))=Акк(0,3)=4.
6.34.
Скласти алгоритм обчислення суми:
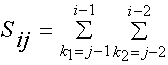 ...
... 
6.35. Ханойськi вежі. Дошка має три стрижні. На перший нанизано N дискiв спадного догори
дiаметра. Потрiбно, перекладаючи
диски по одному, розмiстити їх в початковому
порядку на другому стрижнi. При цьому
бiльший диск нiколи не повинен розмiщуватись над меншим.
Скласти
пiдпрограму, яка iлюструє порядок
перемiщення дискiв. Викликати її при
N=3.
Підрахувати кiлькiсть ходiв, які потрiбнi для перемiщення дискiв. Знайти її залежнiсть вiд N.
Розв`язок. Припусимо, що ми вмiємо переносити N-1 диск. Тодi правило перемiщення N дискiв iз стрижня А на стрижень В з використанням стрижня С для тимчасового зберігання дискiв можна записати таким чином:
1)перенести N-1 диск з А на С;
2)перенести 1 диск з А на В;
3)перенести N-1 диск з С на В.
Очевидно алгоритм має зміст при N>1. Одержуємо
рекурсивну процедуру
процедура Ханой(арг N,А,В,С:нат) це
поч
якщо
N>0 то
Ханой(N-1,А,С,В);
показати(А,`® `,В);
Ханой(N-1,С,В,А)
кр
кп.
яку можна
викликати так: Ханой(N,1,2,3).
При N=3
одержимо 1® 3, 1 ® 2, 3® 2, 1® 3, 2® 1, 2® 3, 1® 3.
Кiлькiсть
ходiв, потрiбних для перемiщення 3 дискiв, дорiвнює 7, для N дискiв - ![]()
6.36. Скласти алгоритм, який вiдображає всi перестановки цiлих чисел вiд 1 до N.
Вказiвка. Множину перестановок цiлих чисел вiд 1 до N можна отримати з множини всiх перестановок цiлих чисел вiд 1 до N-1, вставляючи N в усi можливi позицiї в кожнiй перестановцi.