11

[ЗМІСТ] [Назад] [Початок розділу]

11.4 Проект „Опукла оболонка”

Розглянемо об’єктно-орієнтований проект для розв’язку задачі побудови опуклої оболонки множини точок. Задача формулюється так: є послідовність точок площини, заданих своїми координатами. Треба побудувати опуклу оболонку цієї послідовності точок, показати її а також обчислити її площу та периметр. Проект будемо реалізовувати у Паскалі.

В залежності від заданої послідовності точок їх опукла оболонка може мати вид:

1. Порожня оболонка („нулькутник”).

2. Одноточкова оболонка („однокутник”).

3. Двоточкова оболонка (відрізок або „двокутник”).

4. Опуклий многокутник.

Види опуклих оболонок зображено на Рис 11.2 а) – г).

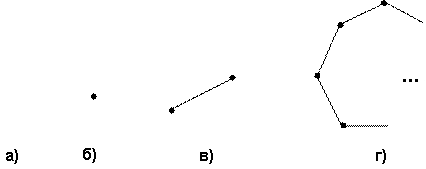
Рис. 11.2 – Види опуклих оболонок

Визначимо класи для реалізації нашого проекту. Для роботи з точками та відрізками на площині нам знадобляться відповідні класи, які ми назвемо Point та Segment. Для кожного виду опуклої оболонки (1-4) визначимо свій клас: Convex, OneConv, TwoConv та Polygon. Вершини многокутника будемо зберігати у деку, для чого використаємо описаний раніше клас деку довільних об’єктів Deque. Оскільки ми використовуємо дек довільних об’єктів, в якому будуть зберігатися точки, класи Point та Segment будуть нащадками AnyObject. Загальна ієрархія класів опуклої оболонки наведена на Рис. 11.3.

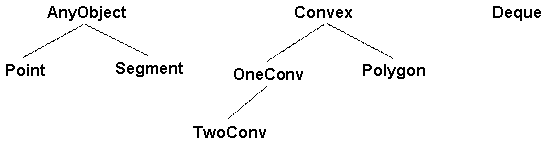
Рис. 11.3 – Ієрархія класів опуклої оболонки

Polygon не є нащадком TwoConv, як того можна було б очікувати, тому що ці класи мають мало спільного. Так само Segment не є нащадком Point.

Класи Point та Segment описані та реалізовані у модулі Geom. Клас Point є нащадком AnyObject та має властивості X,Y – координати точки та методи Init – створити точку з координатами TX,TY; GetX, GetY – отримати координати X та Y; деструктор Done. Наведена нижче реалізація методів класу Point є дуже простою.

Клас Segment є більш складним. Він містить дві властивості – точки A, B, які визначають кінці відрізку та самі є об’єктами класу Point. Клас Segment містить також методи: конструктор Init; GetA, GetB – отримати точки A та B; Len – довжина відрізку; OnLine – чи лежить точка T на одній прямій з відрізком; Into – чи лежить точка T всередині відрізку; Square – площа відрізку зі знаком; деструктор Done.

У конструкторі Init класу Segment ми не можемо присвоїти A:=T1 або B:=T2, тому що A та B – це об’єкти класу Point, який містить віртуальні методи. Тому треба спочатку викликати конструктор Init класу Point (A.Init(T1.GetX,T1.GetY); B.Init(T2.GetX,T2.GetY);). Аналогічно робимо у методах GetA, GetB для точки T. Довжина відрізку – це просто відстань між A та B. Що ж стосується площі, то метод Square обчислює площу S DTAB як значення детермінанту

1 |1 1 1|

S = -*|T_x A_x B_x|

2 |T_y A_y B_y|

Знак цього значення („+” або „-”) залежить від взаємного розташування точок T, A та B. Якщо вважати відрізок AB вектором, спрямованим з точки A у точку B, то площа трикутника DT₁AB (Рис. 11.4) зі знаком буде мати знак „+”, а площа трикутника DT₂AB зі знаком буде мати знак „-”.

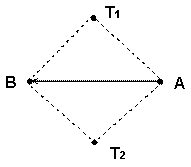
Рис. 11.4 – Різні випадки взаємного розташування точки та відрізку

Метод Square ми будемо, зокрема, використовувати для того, щоб визначити чи лежить точка всередині многокутника. Метод OnLine перевіряє, чи лежить точка T на одній прямій з відрізком AB. Для перевірки ми використовуємо метод Square. Але через наближені обчислення для дійсних чисел ми не можемо перевіряти рівність площі 0. Натомість перевіряємо, чи близьке значення площі до 0 з деякою точністю delta, яку ми вважаємо достатньою. Метод Into використовує два допоміжних відрізки: s1 – відрізок AT та s2 – відрізок TB. Якщо точка T лежить на одній прямій з відрізком AB та довжина кожного з відрізків s1, s2 не більша довжини відрізку AB, то точка T лежить всередині відрізку AB.

{ Модуль роботи з точками та відрізками на площині }

Unit Geom;

interface

Uses AnyThing;

Type

PointRef = ^Point;

Point = Object(AnyObject) { точка площини }

private

X,Y: Real; { координати }

public

Constructor Init(TX,TY: Real); { створити точку }

Function GetX: Real; { координата X }

Function GetY: Real; { координата Y }

Destructor Done; Virtual; { деструктор }

end;

SegmentRef = ^Segment;

Segment = Object(AnyObject) { відрізок на площині }

private

A,B: Point; { кінці відрізку }

public

Constructor Init(T1,T2: Point); { створити відрізок }

Procedure GetA(VAR T: Point); { точка A }

Procedure GetB(VAR T: Point); { точка B }

Function Len: Real; { довжина відрізку }

Function OnLine(T: Point): Boolean;{ чи лежить точка T на одній прямій з відрізком ? }

Function Into(T: Point): Boolean; { чи лежить точка T всередині відрізку ? }

Function Square(T: Point): Real; { площа трикутника TAB зі знаком }

Destructor Done; Virtual; { деструктор }

end;

implementation

Constructor Point.Init;

begin

X:=TX; Y:=TY

end;

Function Point.GetX: Real;

begin GetX:=X end;

Function Point.GetY: Real;

begin GetY:=Y end;

Destructor Point.Done;

begin end;

Constructor Segment.Init;

begin

A.Init(T1.GetX,T1.GetY);

B.Init(T2.GetX,T2.GetY);

end;

Procedure Segment.GetA;

begin

T.Init(A.GetX,A.GetY)

end;

Procedure Segment.GetB;

begin

T.Init(B.GetX,B.GetY)

end;

Function Segment.Len: Real;

begin

Len:=Sqrt(Sqr(A.GetX-B.GetX)+Sqr(A.GetY-B.GetY))

end;

Function Segment.Square;

begin

Square:=0.5*(A.GetX*B.GetY-B.GetX*A.GetY+B.GetX*T.GetY

-T.GetX*B.GetY+T.GetX*A.GetY-A.GetX*T.GetY)

end;

Function Segment.OnLine;

const delta = 0.001;

begin

OnLine:=abs(Segment.Square(T)) <= delta

end;

Function Segment.Into;

var a1,b1: Point; s1,s2: Segment; l: Real;

begin

Segment.GetA(a1); s1.Init(a1,T);

Segment.GetB(b1); s2.Init(b1,T);

l:=Segment.Len;

Into:=Segment.OnLine(T) and (l >= s1.Len) and (l >= s2.Len)

end;

Destructor Segment.Done;

begin end;

end.

Класи, що безпосередньо реалізують опуклу оболонку, описані у модулі Conv. Цей модуль використовує розглянуті раніше модулі AnyThing, Geom, AnyDeque. Для кожного класу описано також вказівник на об’єкти цього класу. Всі класи у модулі мають віртуальні методи AddPoint - додати точку, Show - показати опуклу оболонку та деструктор Done. Метод AddPoint за поточним видом оболонки та новою точкою T визначає, чи змінюється вид опуклої оболонки. Якщо так, то створюється новий динамічний об’єкт та викликається конструктор відповідного класу (існуючий об’єкт при цьому знищується), якщо ні, то, можливо, змінюються характеристики поточної оболонки, але її вид не змінюється. AddPoint повертає вказівник на новостворений об’єкт або на себе, якщо оболонка не змінює вид. Для того, щоб у реалізації методу отримати доступ до об’єкта, для якого цей метод викликано, у Паскалі використовують ключове слово Self. Відповідно, @Self дає адресу цього об’єкта або вказівник на цей об’єкт. Метод Show показує координати всіх точок опуклої оболонки а також її площу та периметр.

Клас Convex реалізує порожню оболонку. Він має властивості Nangle – кількість кутів, Per, Sq – периметр та площа та методи Init - почати роботу, GetNAngle - отримати кількість кутів, GetPer - отримати периметр, GetSq - отримати площу, AddPoint - додати точку, Show – показати опуклу оболонку, деструктор Done. Метод AddPoint відразу створює новий об’єкт класу OneConv, оскільки додавання будь-якої точки до порожньої оболонки створює одноточкову оболонку.

Клас OneConv є нащадком Convex та реалізує одноточкову оболонку. Він має власну властивість A – точка та методи Init - почати роботу, GetA - отримати точку, AddPoint - додати точку, Show – показати опуклу оболонку, деструктор Done. Метод AddPoint створює новий об’єкт класу TwoConv, якщо нова точка не співпадає з вже існуючою. Інакше AddPoint повертає вказівник на себе.

Клас TwoConv є нащадком OneConv та реалізує двоточкову оболонку. Він має власну властивість B – друга точка та методи Init - почати роботу, GetB - отримати точку B, AddPoint - додати точку, Show – показати опуклу оболонку, деструктор Done. Двокутник вже має периметр, відмінний від 0. Це – довжина відрізку AB, яку ми обчислюємо у конструкторі Init за допомогою методу Len класу Segment. Метод AddPoint створює новий об’єкт класу Polygon, якщо нова точка T не лежить на одній прямій з відрізком AB. Інакше AddPoint розглядає три випадки розташування точки T та відрізку AB на одній прямій (Рис. 11.5). Точка T може лежати або всередині відрізку AB (тоді опукла оболонка не змінюється), або поза відрізком AB ближче до точки A (тоді маємо нову двоточкову оболонку з точками B та T), або поза відрізком AB ближче до точки B (тоді маємо нову двоточкову оболонку з точками A та T).

Рис. 11.5 – Розташування точки та відрізку на одній прямій

Клас Polygon є, безумовно, найскладнішим з точки зору реалізації. Вершини многокутника будемо зберігати у деку. Послідовність вершин у деку будемо підтримувати так, щоб ребра (якщо їх розглядати як вектори) були спрямовані проти годинникової стрілки (Рис. 11.6). У кожний момент часу одне з ребер будемо вважати „поточним”. Нехай це ребро буде спрямоване від точки, що лежить у кінці деку, до точки, що лежить на початку деку.

Рис. 11.6 – Впорядкування вершин многокутника

Для визначення порядку вершин у новому многокутнику (трикутнику) а також для додавання точки до многокутника розглянемо поняття „видимості” ребра многокутника з точки. Будемо вважати, що ребро AB є видимим з точки T, якщо точка T лежить на продовженні ребра AB або у трикутнику TAB ребра (як вектори) спрямовані за годинниковою стрілкою (Рис. 11.7 а) ) та невидимим, якщо T лежить всередині ребра AB або у трикутнику TAB ребра спрямовані проти годинникової стрілки (Рис. 11.7 б) ). Якщо точка T не лежить на одній прямій з AB, то ребро AB є видимим з точки T, якщо площа трикутника TAB зі знаком більша 0. Видимість ребра (відрізку S) з точки T перевіряє булівська функція Visible, яка є внутрішньою функцією модуля Conv та не відноситься до жодного з класів.

Рис. 11.7 – Видимість ребра з точки

Клас Polygon є нащадком Convex та має одну власну властивість Dq – дек та методи Init - почати роботу CurSide - повернути поточне ребро, NextSide – перейти до наступного ребра; PreviousSide – перейти до попереднього ребра, AddPoint - додати точку, Show - показати опуклу оболонку, деструктор Done.

Конструктор Init створює трикутник з точок T₁, T₂, T₃, які не лежать на одній прямій. Треба розташувати точки у деку так, щоб ребра були спрямовані проти годинникової стрілки. Використовуємо 3 допоміжних відрізки: s1 (T₁T₂), s2 (T₁T₃), s3 (T₂T₃) та обчислюємо площу та периметр трикутника. Далі кладемо точку T₂ до початку деку. Якщо ребро T₁T₃ є видимим з точки T₂, то треба покласти точку T₁ до початку деку, а точку T₃ - до кінця деку, інакше – навпаки.

Метод CurSide повертає відрізок, який є поточним ребром многокутника. Щоб не змінювати дек, спочатку беремо точки з нього, а потім кладемо на місце. Методи NextSide та PreviousSide забезпечують переміщення по многокутнику, змінюючи його поточне ребро. Метод Show перекладає по черзі всі точки многокутника з початку деку до кінця деку, показуючи на екрані їх координати. Деструктор Done очищує дек, видаляючи з нього всі точки.

Нарешті, метод AddPoint додає нову точку до многокутника (Рис 11.8). При додаванні нової точки можливі два випадки:

1) точка T лежить всередині многокутника або на одному з його ребер (Рис. 11.8 а) );

2) точка T лежить ззовні многокутника (Рис. 11.8 б) ).

Рис. 11.8 – Додавання точки до многокутника

Якщо маємо випадок 1), то жодне з ребер многокутника не є видимим і опуклу оболонку змінювати не потрібно. У випадку 2) треба зробити такі дії:

· видалити з многокутника всі видимі з точки T ребра (A₁A₂, A₂A₃, A₃A₄);

· додати до многокутника два ребра з точки T до граничних точок (A₁T, TA₄);

· переобчислити кількість кутів, площу та периметр многокутника.

Видалення видимих ребер забезпечується видаленням з деку вершин (A₂, A₃). Додавання ребер – розміщенням у деку нової точки T. Переобчислення кількості кутів n, периметру p та площі s виконується за правилами:

n = n – n_del + 2,

p = p – p_del + l₁ + l₂,

s = s + s_del,

де n_del – кількість видалених ребер, p_del – сумарна довжина ребер, що видаляються (A₁A₂, A₂A₃, A₃A₄), l₁ – довжина відрізку A₁T, l₂ – довжина відрізку TA₄, s_del – сума площ трикутників, які утворює точка T з ребрами, що видаляються (DTA₁A₂ DTA₂A₃, DTA₃A₄).

У методі AddPoint ми враховуємо, що поточне ребро може бути як видимим, так і невидимим з точки T. Тому спочатку пропускаємо всі видимі ребра (якщо такі є). Потім пропускаємо всі невидимі ребра. Після цього ми або пройшли всі ребра та не знайшли ребро, яке є видимим з точки T (це означає, що T лежить всередині многокутника), або поточним є перше видиме з точки T ребро. Якщо T лежить ззовні многокутника, то виконуємо видалення видимих ребер до першого ребра, яке не є видимим з точки T, додавання нових ребер та переобчислення характеристик опуклої оболонки.

{ Модуль опису класів опуклої оболонки }

Unit Conv;

interface

Uses AnyThing, Geom, AnyDeque;

Type

ConvRef = ^Convex;

Convex = Object { нулькутник }

private

NAngle: Integer; { кількість кутів }

Per,Sq: Real; { периметр та площа }

public

Constructor Init; { почати роботу }

Function GetNAngle: Integer; { кількість кутів }

Function GetPer: Real; { периметр }

Function GetSq: Real; { площа }

Function AddPoint(T: Point): ConvRef; Virtual;{ додати точку }

Procedure Show; Virtual; { показати }

Destructor Done; Virtual; { закінчити роботу }

end;

OneRef = ^OneConv;

OneConv = Object(Convex) { однокутник }

private

A: Point; { точка }

public

Constructor Init(T: Point); { почати роботу }

Procedure GetA(Var T: Point); { точка A }

Function AddPoint(T: Point): ConvRef; Virtual;{ додати точку }

Procedure Show; Virtual; { показати }

Destructor Done; Virtual; { закінчити роботу }

end;

TwoRef = ^TwoConv;

TwoConv = Object(OneConv) { двокутник }

private

B: Point; { друга точка }

public

Constructor Init(T1,T2: Point); { почати роботу }

Procedure GetB(Var T: Point); { точка B }

Function AddPoint(T: Point): ConvRef; Virtual;{ додати точку }

Procedure Show; Virtual; { показати }

Destructor Done; Virtual; { закінчити роботу }

end;

PolyRef = ^Polygon;

Polygon = Object(Convex) { многокутник }

private

Dq: Deque; { дек точок }

public

Constructor Init(T1,T2,T3: Point); { почати роботу }

Procedure CurSide(Var S: Segment); { поточне ребро }

Procedure NextSide; { наступне ребро }

Procedure PreviousSide; { попереднє ребро }

Function AddPoint(T: Point): ConvRef; Virtual;{ додати точку }

Procedure Show; Virtual; { показати }

Destructor Done; Virtual; { закінчити роботу }

end;

implementation

Constructor Convex.Init;

begin

NAngle:=0; Per:=0; Sq:=0

end;

Function Convex.GetPer;

begin

GetPer:=Per

end;

Function Convex.GetNAngle;

begin

GetNAngle:=NAngle

end;

Function Convex.GetSq;

begin

GetSq:=Sq

end;

Function Convex.AddPoint;

var p: OneRef;

begin

p:=ConvRef(@Self);

AddPoint:=New(OneRef,Init(T)); { почати роботу однокутника }

dispose(p,Done);

end;

Procedure Convex.Show;

begin

writeln('P = ',Per:7:1);

writeln('S = ',Sq:7:1);

end;

Destructor Convex.Done;

begin end;

Constructor OneConv.Init;

begin

Convex.Init; NAngle:=1;

A.Init(T.GetX,T.GetY);

end;

Procedure OneConv.GetA;

begin

T.Init(A.GetX,A.GetY)

end;

Function OneConv.AddPoint;

var p: OneRef;

begin

p:=OneRef(@Self);

if (A.GetX <> T.GetX) or (A.GetY <> T.GetY) then begin

AddPoint:=New(TwoRef,Init(A,T)); { почати роботу двокутника }

dispose(p,done) end

else AddPoint:=p

end;

Procedure OneConv.Show;

begin

writeln('( ',A.GetX:7:1,',',A.GetY:7:1,' )');

Convex.Show;

end;

Destructor OneConv.Done;

begin end;

Constructor TwoConv.Init;

var s: Segment;

begin

OneConv.Init(T1); NAngle:=2;

B.Init(T2.GetX,T2.GetY);

s.Init(A,B); Per:=s.Len;

end;

Procedure TwoConv.GetB;

begin

T.Init(B.GetX,B.GetY)

end;

Function TwoConv.AddPoint;

var s,s1,s2: Segment;

p: TwoRef;

begin

p:=TwoRef(@Self);

s.Init(A,B); s1.Init(A,T); s2.Init(B,T);

if s.Online(T) then { точки T,A,B на одній прямій ? }

begin

if s1.Into(B) then B:=T { точка B лежить всередині A,T ? }

else if s2.Into(A) then A:=T; { точка A лежить всередині B,T ? }

s.Init(A,B); Per:=s.Len; AddPoint:=p

end

else begin

AddPoint:=New(PolyRef,Init(A,B,T)); { почати роботу многокутника }

dispose(p,done)

end

end;

Procedure TwoConv.Show;

begin

writeln('( ',B.GetX:7:1,',',B.GetY:7:1,' )');

OneConv.Show;

end;

Destructor TwoConv.Done;

begin end;

Function Visible(S: Segment; T: Point): Boolean;

begin

Visible:=(S.Online(T) and not S.Into(T)) or (S.Square(T) > 0)

end;

Constructor Polygon.Init;

var s1,s2,s3: Segment;

begin

s1.Init(T1,T2); s2.Init(T1,T3); s3.Init(T2,T3);

NAngle:=3; Per:=s1.Len+s2.Len+s3.len; Sq:=abs(s1.Square(T3));

Dq.Init;

Dq.PutBg(New(PointRef,Init(T2.GetX,T2.GetY))); { покласти T2 до початку }

if Visible(s2,T2) then { ребро T1,T3 видиме з точки T2 ? }

begin

Dq.PutBg(New(PointRef,Init(T1.GetX,T1.GetY))); { покласти T1 до початку }

Dq.PutEn(New(PointRef,Init(T3.GetX,T3.GetY))) { покласти T3 до кінця }

end

else

begin

Dq.PutBg(New(PointRef,Init(T3.GetX,T3.GetY))); { покласти T3 до початку }

Dq.PutEn(New(PointRef,Init(T1.GetX,T1.GetY))) { покласти T1 до кінця }

end

end;

Procedure Polygon.CurSide;

var p1,p2: PointRef;

begin

p1:=PointRef(Dq.GetEn); p2:=PointRef(Dq.GetBg);

S.Init(p1^,p2^);

Dq.PutEn(p1); Dq.PutBg(p2)

end;

Procedure Polygon.NextSide;

begin

Dq.PutEn(Dq.GetBg);

end;

Procedure Polygon.PreviousSide;

begin

Dq.PutBg(Dq.GetEn);

end;

Function Polygon.AddPoint;

var s: Segment; p: PointRef;

ndel,i: Integer; vis: Boolean;

pdel: Real; {сумарна довжина ребер, що видаляються}

sdel: Real; {площа над ребрами, що видаляються}

begin

Polygon.CurSide(s); vis:=Visible(s,T);

i:=1;

while (i <= NAngle) and vis do begin { пропустити видимі ребра }

Polygon.NextSide; Polygon.CurSide(s);

vis:=Visible(s,T); i:=i+1

end;

while (i <= NAngle) and not vis do begin { пропустити невидимі ребра }

Polygon.NextSide; Polygon.CurSide(s);

vis:=Visible(s,T); i:=i+1

end;

if vis then begin

ndel:=1; pdel:=s.Len; sdel:=s.Square(T);

while true do begin { видалити видимі ребра з многокутника }

Polygon.NextSide; Polygon.CurSide(s);

if not Visible(s,T) then break;

ndel:=ndel+1; pdel:=pdel+s.Len; sdel:=sdel+s.Square(T);

p:=PointRef(Dq.GetEn); dispose(p,Done);

end;

Polygon.PreviousSide; {повернутися на крок назад}

Dq.PutBg(New(PointRef,Init(T.GetX,T.GetY))); { покласти T до початку }

Polygon.CurSide(s); Per:=Per-pdel+s.Len;

Polygon.NextSide; Polygon.CurSide(s); Per:=Per+s.Len;

NAngle:=NAngle-ndel+2; Sq:=Sq+sdel;

end;

AddPoint:=@Self

end;

Procedure Polygon.Show;

var p: PointRef; i: Integer;

begin

for i:=1 to NAngle do begin

p:=PointRef(Dq.GetBg);

writeln('( ',p^.GetX:7:1,',',p^.GetY:7:1,' )');

Dq.PutEn(p);

end;

Convex.Show;

end;

Destructor Polygon.Done;

begin

Dq.Clear

end;

end.

Програма ConvCalc створює опуклу оболонку як динамічний об’єкт, організовує введення послідовності координат точок, що додаються до опуклої обоолонки, показує опуклу оболонку, після чого знищує її. Введення послідовності координат точок здійснюється до кінця стандартного вхідного файлу input (до натиснення комбінації клавіш <Ctrl>+<Z>). Оскільки методи AddPoint, Show, Done є віртуальнимим, обробка опуклої оболонки здійснюється незалежно від її виду.

Program ConvCalc;

Uses AnyThing,Geom,AnyDeque,Conv;

Var

cv: ConvRef;

t: Point; x,y: Real;

begin

writeln('Введіть послідовність точок для побудови опуклої оболонки');

New(cv,Init); { почати роботу з опуклою оболонкою }

while true do begin { цикл с виходом }

write('Введіть координати точки: '); Readln(x,y);

if eof then break; { якщо кінець введення, то вихід }

t.Init(x,y);

cv:=cv^.AddPoint(t); { додати точку }

end;

writeln('Опукла оболонка:');

cv^.Show; { показати опуклу оболонку }

dispose(cv,Done); { видалити опуклу оболонку }

end.

Задачі та вправи

Вправа 11.1. Реалізувати методи PutEn та GetEn для деків у Паскалі та C++.

Вправа 11.2. Реалізувати проект „опукла оболонка” у мові C++.

Вправа 11.3. Реалізувати додатковий клас (класи) та змінити реалізацію методів Show (можливо, додати нові властивості) для показу опуклої оболонки у графічному режимі.

[ЗМІСТ] [Назад] [Початок розділу]