[ЗМІСТ] [Далі] [Назад] [Початок розділу]

10.5. Дерева та графи

Стеки, черги та деки, списки є лінійними або одновимірними структурами даних. Дерева та графи є прикладами плоских або двовимірних структур. Дамо декілка означень.

Орієнтованим графом G називають пару множин V, U

G = (V, U),

де V – множина вершин, а U – множина дуг. Дуга з’єднує дві вершини графа.

Далі орієнтовані графи будемо називати просто графами. Приклад графа зображено на Рис. 10.29. Цей граф має 4 вершини з номерами від 1 до 4. Дуги з’єднують вершини 1 та 2, 2 та 1, 2 та 3, 4 та 4. Вершини графа також називають вузлами.

Рис. 10.29 – Граф

Якщо дуга u виходить з вершини v₁ та входить у вершину v₂, то кажуть, що v₂ безпосередньо слідує з v₁. Позначати це будемо так:

u

v₁ ú¾® v₂ або просто, v₁ ú¾® v₂

Шлях у графі G з вершини v₀ у вершину v_n – це послідовність вершин v₀, v₁, v₂, ... v_n-1, v_n така, що

v₀ ú¾® v₁, v₁ ú¾® v₂, ..., v_n-1 ú¾® v_n

Шлях будемо позначати v₀ ¾® v_n. Якщо існує шлях між вершинами v₀ та v_n, кажуть, що v_n слідує з v₀. На Рис. 10.29 існують шляхи з 1 до 3, з 1 до 1, з 4 до 4 тощо. Довжина шляху у графі – це кількість вершин, які входять у шлях.

Шлях між вершинами v₀ та v_n називається циклом, якщо v₀ = v_n. Граф на Рис. 10.29 має цикли з 1 до 1, з 2 до 2 та з 4 до 4.

Граф G називають незв’язним, якщо існує розбиття множини вершин V на дві множини V₁, V₂ такі, що:

V₁ È V₂ = V, V₁ Ç V₂ = Æ,

u₁ u₂

"v₁ Î V₁, v₂ Î V₂ не існує u₁, u₂ Î U таких, що v₁ ú¾® v₂ або v₂ ú¾® v₁

Іншими словами, граф називають незв’язним, якщо всі його вершини можна розбити на дві підмножини вершин, між яким не проходить жодна дуга. Граф на Рис. 10.30 є незв’язним, бо існує розбиття на дві підмножини вершин {1, 2, 3} та {4}, між якими не проходить жодна дуга.

Граф G називають зв’язним, якщо він не є незв’язним.

Рис. 10.29 – Розбиття вершин незв’язного графа на дві підмножини

Напівстепінь входу вершини графа v – це кількість дуг, які входять у дану вершину. Напівстепінь виходу вершини графа v – це кількість дуг, які виходять з даної вершини. Вершина з напівстепінню входу 0 називається джерелом, а вершина з напівстепінню виходу 0 – стоком.

Часто вважають, що у вершині графа зберігаються дані. Такі дані називають навантаженням вершини.

Деревом називають зв’язний граф з одним джерелом та напівстепінню входу всіх вершин не більше 1. Дерева зображують, починаючи від джерела, вниз. Стрілки у дугах, як правило, опускають (Рис. 10.30).

Рис. 10.30 – Дерево

Єдине джерело називають коренем дерева. Стоки у дереві називають листям дерева. Будь-який шлях у дереві називають гілкою дерева. Будь-яка частина дерева, яка сама є деревом, називається піддеревом. Вершини, які безпосередньо слідують з даної, називаються синами даної вершини, а сама ця вершина – їх бітьком. Синами називають також не тільки самі вершини, що безпосердньо слідують з даної, але й піддерева, для яких ці вершини є коренями. Будь-які два сини однієї вершини називають братами. Дерево, яке не вміщує вершин, називається порожнім деревом. Висотою дерева називають довжину найдовшого шляху (найдовшої гілки) у дереві.

Бінарним деревом називається дерево з напівстепінню виходу всіх вершин не більше 2. Впорядкованим бінарним деревом називається бінарне дерево, кожна вершина якого завжди має 2 сини: лівий син та правий син, які можуть бути порожніми або непорожніми деревами (Рис. 10.31). Далі будемо розглядати тільки впорядковані бінарні дерева.

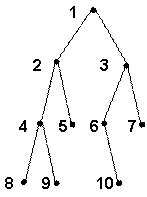
Рис. 10.31 – Впорядковане бінарне дерево

10.5.1 Бінарне дерево

Визначимо операції, відношення та інструкції для бінарних дерев:

1. Почати роботу.

2. Чи порожнє дерево?

3. Створити дерево.

4. Корінь дерева.

5. Лівий син.

6. Правий син.

Дії 1, 3, 4, 5, 6 – операції; 2 – відношення.

Операція “Почати роботу” повертає порожнє дерево.

“Створити дерево” – за двома деревами t₁, t₂ та даними n створити бінарне дерево з коренем з навантаженням n, лівим сином t₁ та правим сином t₂.

“Корінь дерева” повертає навантаження кореня дерева. Дерево при цьому не змінюється. Для порожнього дерева ця операція повинна давати відмову.

“Лівий син” повертає піддерево, яке є лівим сином дерева. Лівий син порожнього дерева за означенням – порожнє дерево.

“Правий син” повертає піддерево, яке є правим сином дерева. Правий син порожнього дерева за означенням – порожнє дерево.

Можлива реалізація бінарного дерева з використанням вказівників зображена на Рис. 10.32. Вершини дерева – це записи з трьох полів: поле даних та вказівники на лівого та правого синів. За допомогою вказівників вершини дерева з’єднані між собою. У листі дерева вказівники на лівого та правого синів дорівнюють nil. Саме дерево – це вказівник на корінь. Якщо дерево порожнє, то вершин немає, а вказівник дорівнює nil.

Рис. 10.32 – Реалізація бінарного дерева

Розглянемо модуль реалізації бінарних дерев у Паскалі. Треба зазначити, що всі дії реалізовані за допомогою функцій. Функції Init, Empty, Root, LeftSon залишаються для самостійної роботи. Функція MakeTree (Рис. 10.33) схожа на функцію додавання елемента у класичний список. Функція RightSon повертає nil для порожнього дерева або вказівник на правого сина непорожнього.

unit IntBTree;

interface

type btree = ^telem; {Дерево}

telem = record {Елемент дерева}

d: integer;

rs, ls: btree

end;

function Init: btree; { Почати роботу }

function Empty(t: btree): boolean; { Чи порожнє дерево? }

function MakeTree(n: integer; t1, t2: btree): btree;{ Створити дерево }

function Root(t: btree): integer; { Корінь дерева }

function LeftSon(t: btree): btree; { Лівий син }

function RightSon(t: btree): btree; { Правий син }

implementation

.................

function MakeTree(n: integer; t1, t2: btree): btree;

var p: btree;

begin

new(p);

p^.d:=n;

p^.ls:=t1; p^.rs:=t2;

MakeTree:=p

end;

.................

function RightSon(t: btree): btree;

begin

if t=nil then RightSon:=nil

else RightSon:=t^.rs

end;

end.

Рис. 10.33 – Створення дерева

Наша реалізація бінарних дерев, як і реалізація класичних списків, є дуже простою, але не економить динамічну пам’ять.

Стандартною задачею для бінарних дерев є обхід дерева (обхід всіх вершин дерева) та обробка кожної вершини. Такий обхід, як і більшість задач з використанням дерев, виконується рекурсивними підпрограмами. Виділяють декілька способів обходу бінарних дерев: КЛП (корінь, лівий син, правий син), ЛКП (лівий син, корінь, правий син) та ЛПК (лівий син, правий син, корінь). При КЛП-обході спочатку обробляють корінь дерева, потім проходять лівого сина, а потім – правого сина. При ЛКП-обході спочатку проходять лівого сина, потім обробляють корінь дерева, а потім проходять правого сина. При ЛПК-обході спочатку проходять лівого сина, потім проходять правого сина, а потім обробляють корінь дерева. Послідовність проходу вершин для бінарного дерева, що зображене на Рис. 10.31, для різних типів обходу наведена нижче:

КЛП – 1, 2, 4, 8, 9, 5, 3, 6, 10, 7

ЛКП – 8, 4, 9, 2, 5, 1, 6, 10, 3, 7

ЛПК – 8, 9, 4, 5, 2, 10, 6, 7, 3, 1

Як приклад використання бінарних дерев наведемо програму, яка підраховує кількість вузлів дерева а також друкує навантаження вершин дерева у порядку проходу для різних типів обходу дерева. Функція NodeCount підраховує кількість вузлів дерева. Процедури PrtKLP, PrtLKP та PrtLPK показують порядок проходу вершин для КЛП-, ЛКП- та ЛПК-обходів. Основна програма створює дерево, яке зображено на Рис. 10.34, та показує результати.

Рис. 10.34 – Бінарне дерево, що створює програма BtreeTst

program BtreeTst;

uses IntBTree;

function NodeCount(t: btree): word;

begin

if Empty(t) then NodeCount:=0

else

NodeCount:=1+NodeCount(LeftSon(t))+NodeCount(RightSon(t))

end;

procedure PrtKLP(t: btree);

begin

if Empty(t) then write(' ,')

else begin

write(Root(t),',');

PrtKLP(LeftSon(t));

PrtKLP(RightSon(t))

end

end;

procedure PrtLKP(t: btree);

begin

if Empty(t) then write(' ,')

else begin

PrtLKP(LeftSon(t));

write(Root(t),',');

PrtLKP(RightSon(t))

end

end;

procedure PrtLPK(t: btree);

begin

if Empty(t) then write(' ,')

else begin

PrtLPK(LeftSon(t));

PrtLPK(RightSon(t));

write(Root(t),',');

end

end;

var t: btree;

begin

t:=MakeTree(1,MakeTree(2,MakeTree(3,Init,Init),MakeTree(4,Init,Init)),

MakeTree(5,MakeTree(6,Init,Init),Init));

writeln;

writeln('Число вузлів ',NodeCount(t));

write('КЛП='); PrtKLP(t); writeln;

write('ЛКП='); PrtLKP(t); writeln;

write('ЛПК='); PrtLPK(t); writeln;

end.

В результаті роботи програми BtreeTst на екрані буде показано:

Число вузлів 6

КЛП=1,2,3, , ,4, , ,5,6, , , ,

ЛКП= ,3, ,2, ,4, ,1, ,6, ,5, ,

ЛПК= , ,3, , ,4,2, , ,6, ,5,1,

На завершення розгляду бінірних дерев наведемо файл заголовку модуля бінарного дерева у мові Сі.

/* Бінарне дерево btree.h */

typedef struct telem *btree; /* Дерево */

struct telem { /* Елемент дерева */

int d;

btree ls, rs;

};

extern btree init(); /* Почати роботу */

extern int empty(btree t); /* Чи порожнє дерево? */

extern btree make(int n, btree t1, btree t2); /* Створити дерево */

extern int root(btree t); /* Корінь дерева */

extern btree leftson(btree t); /* Лівий син */

extern btree rightson(btree t); /* Правий син */

[ЗМІСТ] [Далі] [Назад] [Початок розділу]